公式サイトトップ>> 数学の個別指導|医学部,難関大受験対策
医学部,難関大合格へ導く数学の個別指導
医学部,難関大に合格するためには、国公立でも私大でも配点が高く、 本番での得点差がつきやすい数学を得意科目にすることが合格可能性を大きく高めることは事実です。
しかしながら、数学を得意科目にする、数学で確実に安定して高得点を獲得する 実力をつけるのは一般的な予備校さんや塾さんの指導では非常に難しいのです。
その理由は、数学を得意科目にするために必要なのは、明確な思考と論理を確立することなのですが、 この部分について、 一般的には出来る人の「感覚」として語られたり、実際に受験数学で高得点をとっていない人が 指導に当たっていることも非常に多く、 的確なものを受験生が得られない状況にあるからです。
数学を得意科目にする、数学で安定した高得点を獲得するための指導、 個別指導とはどういったものなのか、 そしてそれがなぜ世の中にはほとんど存在せずに 一部の人しか得られていないのかについてもこのコンテンツを読むことで実感していただければと思います。
当塾指導は、マンツーマンの初回指導における年間計画の策定で各自の状況に応じて、 各自が学校で使用している、またはそれまで使用してきた問題集や参考書を できるだけ活かす形で計画を立てます。 (これが最も受講生にとって効率的に実力をつけていける手段だからです)
その後、各自が使用する、その問題集や参考書についてわからない問題やわからない部分について全教科の質問回答指導、説明指導、添削指導を行っています。 したがって、質問回答している教材は、市販の問題集・参考書のほとんど、過去問に至っては全国のほとんどの大学の問題に及びます。
たった一日で数百という数の問題の質問回答がたまります。 しかも、それは受験数学を極めた東大理三合格講師陣の回答です。 掲載できるのはごくごく一部ですが、優れた数学の個別指導の威力を十分体感していただけると思います。
【目次】数学の個別指導の実際の質問回答
【目次】クリックで質問,回答へ飛べます
グラフの交点の個数から解の数を求めるような問題で、どのようにして交点の個数を判断すればよいですか
図形の問題で場合分けが必要なとき,どのような基準で判断すればよいか
二次関数がある範囲で2つの解を持つ条件は,どのように整理すればよいか
軌跡・領域の問題で、最後に除外点があるかどうかを判別する方法はあるか?
空間図形の求積問題で図形をイメージできずに時間がかかってしまうがどうすればいいか。
適宜更新をして質問回答を今後大量に出していきます。
指導内容・コース・受講料の詳細はこちらから▼
質問回答を有効活用していただくための3つのポイント!
注意1
実際に受講生からいただくご質問には教科書、問題集、参考書、過去問集の該当の問題の全文の画像がありますが、ここでは割愛させていただきます。
受講生からのご質問については、著作権上実際の問題集の問題をそのまま使用できませんので、
ほとんどのご質問および回答をここに掲載するために一般化していることをあらかじめご了承ください。
(実際には問題集や過去問などの具体的な問題のご質問に具体的数値や具体的状況に応じたきめ細やかな回答、解説を行っています。)
【最重要視点】
個別具体的な問題の解法を掲載しそれを詳しく解説することは極めて容易なことです。数百でも数千でもいくらでも掲載できます。しかし、そんなものをいくら見たところで、集めたところで、それは問題の数だけ解法や解法へのアプローチを学んでいるにすぎず、個々的な問題に対しての解法や解法へのアプローチを集めているだけです。これは初見の問題に対しては全くの無力です。そんなものゴミです。初見の問題を解けるようにならない解説なんて何の役にも立ちません。
これにちゃんと気づけている受験生が狭き門をかいくぐり合格を手にする受験生であり合格の天使のポストやコンテンツを見ていただいている受験生です。
具体→抽象→一般化
これが問題を学ぶ際の重要思考作業です。
一般化された知識→具体的問題への還元
これが初見の問題を解く際の重要思考作業です。
このためにあえて合格の天使のコンテンツやポストでは
受講生の質問を一般化
講師の回答も一般化
受講生の質問を一般化
講師の回答も一般化
しているのです。
これは合格の天使の指導でも同じです。
まず受講生がわからない個別具体的な問題を説明・解説する。でもその問題だけでなく関連問題やその分野の問題を解けるように一般化した説明・解説も加える。これにより初見の問題にも効率的に対処していけるようになるのです。
ただこれは実力的にもノウハウ的にも誰にでもできる解説ではありません。
選別され、かつ、「専属契約」で2008年創業以来のノウハウを共有している合格の天使の東大理三合格講師陣からこの部分の非常に優れたものを得ることができるのが合格の天使の受講生なのです。
また、著作権などの法令遵守の観点から合格の天使では安易に問題集の問題や過去問そのものや自作でない図形、画像をポストなどに掲載しないようにしています。これは本来当然のことです。
指導側の都合、利益ではなく受験生にとって合格に必要なものをご提供する。 受験指導機関である以上法令遵守は当たり前。 これが合格の天使の理念です。
注意2
当塾指導は受講生の現在の理解レベルや状況に応じて質問回答を行います。
入塾試験を課していないため受講生の実力はバラバラです。
そのため極めて基本的なご質問およびそれに対する回答も丁寧に行います。
簡潔に表現すると合格の天使の指導は「質問回答もオーダーメイド」です。
同じ分野や同じ問題の質問でも受講生によって回答レベルを変えています。
当塾の徹底指導の理念及び単なる東大理三合格者ではない人柄も優れた東大理三合格講師集団だからなせる指導です。
この点も考慮して回答をご覧ください。
注意3
ここに掲載する回答は、毎日受講生から頂く多くのご質問に対するごくごく一部をご紹介するものです。
すなわち、1人の受講生が1日に数問~10問程度の質問、1日トータルで百~数百問、1か月で数千~数万問、1年で数万~数十万問、数年で数十万~数百万問という膨大な数の質問回答の中からランダムに1問ずつ取り上げて掲載するものです。
漸化式の統一された解き方
受講生の質問
漸化式の統一された解き方はないのですか?
回答
グラフの交点の個数から解の数を求めるような問題
受講生の質問
グラフの交点の個数から解の数を求めるような問題で、どのようにして交点の個数を判断すればよいですか
回答
図形の問題で場合分けが必要なとき
受講生の質問
図形の問題で場合分けが必要なとき,どのような基準で判断すればよいか
回答
二次関数がある範囲で2つの解を持つ条件は,どのように整理すればよいか
受講生の質問
二次関数がある範囲で2つの解を持つ条件は,どのように整理すればよいですか
回答
軌跡・領域の問題で、最後に除外点があるかどうかを判別する方法はあるか?
受講生の質問
軌跡・領域の問題で、最後に除外点があるかどうかを判別する方法はありますか?
回答
ベクトルの問題で内積を利用するタイミング
受講生の質問
円周上の3点を頂点とする三角形について、aOA+bOB+cOC=0となる条件を用いて面積を求める際に、なぜ内積を利用しなければいけないのか
回答
まずベクトルの問題で内積を利用するタイミングについてですが、大まかに言えば角度が分かっているとうれしい状態で利用することが多いです。
具体的には、辺の長さのみがわかっているがそれ以外に条件が見当たらない時や、角度があれば簡単に解けるがきれいに求まらなそうで、どうしても計算が煩雑になってしまいそうな時などが該当します。
今回の状況で内積を利用する主な理由は、先ほども述べたとおり他に表現することが難しいベクトル間の配置関係を明確にするためです。
内積は二つのベクトルの長さとその間の角度のコサインに依存するため、角度情報を効率的に利用することが可能になります。
このような性質を利用することで、ベクトルは今回のような問題においては点同士の配置がどのようになっているかを具体的に考えることなく答えを求める有力な手段となります。
内積を用いることで、複雑なベクトル同士の位置関係を角度や長さというより直感的な概念に落とし込み、問題を解きやすくすることができます。
そのため、内積はベクトルを扱う問題において非常に強力なツールとなり、円周上の3点を頂点とする三角形の性質を探る際にも欠かせない手法の一つと言えるでしょう。
(二次式×等比数列)型の和を求めるやり方
受講生の質問
(二次式×等比数列)型の和を求めるやり方教えてください
回答
(等差数列×等比数列)型はみなさん解けると思います。
例えば、a_n¬=n・2^n の計算はみなさんできますよね。
和Sに対して2倍した2Sを作り、2S–Sを計算するのでした。
そうすると等比数列に帰着できました。
では、なぜ公比倍するのかというと、nの項が消えるからです。
階差数列型の漸化式を解くときに添え字(番号、インデックスともいう)をずらして引き算しますよね?
あれと感覚は一緒です、一つずらして引くことでnがなくなるんです。
しかし、この「nがなくなる」という表現は的確ではありません。
正確には、「nの次数が下がる」です。
実際にa_n¬=n^2・2^nでやってみるとわかります。
2n+1の因子が出てくるはずです。
これはもちろん(n+1)^2-n^2=2n+1に起因するものです。
2次式が1次式になっています。
この状態で同じ作業をもう一度行い1次式を0次式にすると解けます。
並べて引くことで次数を下げる方法は様々な分野で登場する考え方です。
問題の解き方を学んだときに、なぜその解き方で解けるのか、を考えると解放の裏にある原理を理解でき、レベルの上がった問題に応用できます。
コーシーシュワルツの不等式の意味
受講生の質問
コーシーシュワルツの不等式が覚えられないし、そもそも何を意味するのかわからない
回答

公式の図形的イメージ〜三角関数の合成編〜
受講生の質問
三角関数の合成について、なんの目的で合成するのか,結局なにをしているのかイメージできません。
回答
共通テストに向けて
公式の図形的イメージ
〜三角関数の合成編〜

「割り切れる」と「微分」のつながり
受講生の質問
「割り切れる」と「微分」のつながり?
回答
差がつく重要解法。

集合の問題で最大値などを考える問題の解き方(カルノー図)
受講生の質問
集合の問題で最大値などを考える問題が苦手なのですがどのようにして解いていますか。
回答
核となる考え方は「要素の数は負になることはない」です。 リンゴが好きな人が −5人 になることはありえませんね。そこで要素を文字で置いていったときに、0以上であるという条件から最大値最小値を求めます。
ちなみに、あまり知られていないようですがベン図の他にカルノー図というものもあって、こちらは要素の数を把握する場合や集合が4つのときなどに特に有効です。
以下の例題でカルノー図を用いた解法を示しておきます。

定積分を含む不等式評価の⽅法
受講生の質問
定積分を含む不等式評価の⽅法が思いつかない。
回答
定積分が含まれている不等式評価の場合、ただ定積分を計算し、値を求めるだけでは証 明することができないものが多くあります。私はこの種類の問題の解法として2通りあると 考えています。
定積分を含む不等式評価の⽅法
① 被積分関数のグラフをかき、求める部分を他の図形(⻑⽅形、三⾓形、台形)で評価する
② 定積分の中⾝(被積分関数)を別の関数で評価した後に与えられた積分範囲で各辺を積分する
まずは、①についてですが、これは被積分関数が簡単な場合でないと使えない考え⽅であるとわかると思います。特にシグマ和での評価の場合は幅が1の⻑⽅形を⽤い、それ以外の場合は三⾓形や台形での評価をする場合が多いと思います。
次に、②についてですが、かなり発想が難しいように考える⼈も多いと思います。あくまで も経験則になってしまいますが、この⼿の問題の場合、定積分は計算できないものがほとん どです。そこで、複雑な要素(例えば、𝑒 ,𝑠𝑖𝑛𝑥 など)を簡単なもの(例えば、1 ,𝑥 など) で置き換えると定積分が計算でき、それにより不等式評価できるという問題が多いように 感じます。
定積分を含む不等式評価の証明問題は似たような考え⽅を使う問題が多いので、ある程度 の演習を重ねることによって、解きやすくなると思います。
「連続m整数の積はmの倍数である」を利用できる証明
受講生の質問
『全ての自然数nについてn(n+1)(2n+1)は6の倍数であることを示せ』という問題の解答で『n(n+1)(2n+1)=2n(n+1)(n+2)-3n(n+1)』という変形が出てきたが、どういう風に思いついたのか」
回答
まず、変形に気づけなくても、n=6a、n=6a+1、n=6a+2・・・という風に「nを6で割った余りが何か」で場合分けして「n(n+1)(2n+1)」に代入すれば、時間はかかりますが解けますね。また、6の倍数であることを示すには、まず偶数であること、次に3の倍数であることを示せばよいので、先にn=2b、n=2b+1と場合分けして偶数であることを示し、次にn=3c、n=3c+1、n=3c+2と場合分けして3の倍数であることを示す、という手もあります。このように、余りによって分類して証明する基本的な手段があることを認識しておくのがまずは1番大事です。
本題のその変形についてですが、これは、「連続3整数の積は3の倍数である」ということを使おうという明確な目標をもって変形が行われています。(6の倍数であることを示すために、とりあえず3の倍数であることを示せばよさそうだ、と考えています。)「n(n+1)(n+2)」には、nとn+1という連続する2整数が入っているので、それに続くn+2をかけ合わせた「n(n+1)(n+2)」は3の倍数になります。これの最高次(3次)の係数は1ですが、示さなければならない「n(n+1)(2n+1)」の最高次の係数は2なので、n(n+1)(n+2)全体を2倍してあげると、よりn(n+1)(2n+1)に近づけられます。あとはその2n(n+1)(n+2)とn(n+1)(2n+1)の差を計算することで、「n(n+1)(2n+1)=2n(n+1)(n+2)-3n(n+1)」を導くことができます。これによって、n(n+1)という連続2整数の積の項も現れたので、めでたく「2×(3の倍数)-3×(2の倍数)」と変形できたことになり、6の倍数であることが示せます。
この変形しかできないというわけではなく、無限に変形はできます。例えばnとn+1にn-1を付け足して連続3整数の積にした「(n-1)n(n+1)」を使って変形すると「n(n+1)(2n+1)=2(n-1)n(n+1)+3n(n+1)」となりますが、この式の右辺は「2×(3の倍数)+3×(2の倍数)」となっているので、6の倍数であることを示しています。
このように式変形で証明するメリットは、場合分けしなくてよく、計算量も少なくて済むというメリットがありますが、自信をもって使うにはある程度慣れが必要なので、まずは余りによって分類する解法がしっかりとれることが大切です。
解の配置の問題
受講生の質問
解の配置の問題では問題集のように3つの条件(下に書いてあります)にそって解いていくとなっているですが、いくつかの問題では全ての条件を用いてるわけではありません。なんとなく理由がわかる気がするのですが、これはどういうことでしょうか。
条件
①判別式の符号
②軸の範囲
③端点におけるy座標
回答
解の配置の問題として問題集に書いてある3つの条件は絶対に覚えておいてください。 基本的にこれらの3つの条件を使えば必ず問題は解けます。
ただし、いくつかの問題では全ての条件を使う必要はありません。 ではどうやってその判断をしているかと言うとグラフを書いて考えています。
例えば、上に凸の二次関数x**2-2ax+4=0において一つの解が1より小さく、もう1つは1より大きいという問題を考えます。 f(1)という値がマイナスである上に凸の二次関数を書けばわかるのですが、これはどう頑張っても必ずx軸と条件の範囲で2回交わります。これは自分で絵を書いて考えてみてください。よって判別式の条件と軸の条件を使わなくても済み、f(1)を考えるだけでいいです。
他の例として、同じ関数において2解が0~2と2~4の間に一つずつあるという問題を考えましょう。 f(0)が正で、f(2)が負、f(4)が正であれば上に凸の二次関数は必ず条件の範囲で2つの実数解を持ちます。判別式の条件と軸の範囲の条件を気にしなくもいいです。よくわからなかったら自分で色々と絵を書いて確認してみてください。
数学の問題では式だけではなく、図形的に視覚的に捉えることができれば愚直にやらなくても済むため、かなり計算量を減らせます。これが図を書くべき理由です。
鳩の巣原理って何?
受講生の質問
質問:鳩の巣原理って何ですか?受験数学における使われ方を教えてください
回答
鳩の巣原理という概念は、入試数学において時折顔を出す重要なトピックです。これは発想こそ非常にシンプルですが、存在を知っているかどうかで差がつく場合があります。
鳩の巣原理の内容は、簡潔に言えば「n個の物をm個の箱に入れる際、n>mの場合、必ず1つ以上の箱に2つ以上の物が入る」というものです。一見、言われてみれば当たり前のことかもしれません。しかし、この「当たり前」を数学的に明確にすることで、様々な問題を解決する手助けとなります。
例として、「4つの整数があれば、3で割った時の余りが同じ組み合わせが存在する」という主張は、鳩の巣原理を基にした説明ができます。余りのパターンは0, 1, 2の3つしかないのに対し、整数は4つあるため、どこかで余りが重複することは自明です。このように、鳩の巣原理の背後にある思考を頭に入れておくことで、何をもって自明として良いのか、どのようにして証明を進めるべきなのかが明確になります。
さらに、整数問題だけでなく、「差の1の位が0となる組み合わせが存在する」などの問題でも、この原理が有効に働くことがあります。ある一定の範囲内での状況を観察し、鳩の巣原理が適用できるのではないかと仮定することで、解答への道筋が見えてくることも少なくありません。
鳩の巣原理をはじめとする、当たり前のように思える数学的な概念や原理をしっかりと理解することで、数学の問題へのアプローチが変わる可能性があります。これは、他の数学の定理や法則にも共通して言えることでしょう。日常生活の中で何気なく使っている概念でも、それを明確にし、数学的な言語で表現することで、問題解決の手助けとなるのです。
このように、鳩の巣原理はメジャーな概念や派手さがあるツールとは言えないながらも、数学の中でのその役割は大きいです。繰り返し触れ、その背後にある思考を身につけることで、数学的な考え方の幅を広げていくことが非常に大切です。
軌跡を求める問題の記述
受講生の質問
質問:軌跡を求める問題で学校の先生が最初の点Pの(x,y)を大文字で置いたら最後の青で囲った部分 (注:「(与えられた条件を満たす点Pは①上にある。) 逆に①上の任意の点は与えられた条件を満たす。」という文言のこと) を書かなくていいと言っていました。本当に書かなくても大丈夫なのでしょうか?
回答
同値性を維持したまま変形して解いたのでなければ、書く必要があります。 詳細は以下の画像3枚で説明しました。



図形と方程式
受講生の質問
「x^2+y^2<a^2…① を満たす任意の実数x、yに対して、|x+y|+|x-y|<b…② が成り立つとき、正の定数a、bの満たす条件を求めよ。」 という問題についてなのですが、解答の方針が立てられませんでした。
回答
ポイントは「x^2+y^2<a^2...①を満たす任意の実数x,yに対して、|x+y|+|x-y|<b...②が成り立つ」 という条件を座標平面上に落とし込んで考えることです。
まずは問題文を噛み砕いて考えて見ましょう。 x^2+y^2<a^2...①を満たす任意の実数x,yは座標平面上では何に対応しているかというと、 x^2+y^2<a^2の内部の点全体です。

そして|x+y|+|x-y|<b...②が示す領域を図示すると下の図の様になります。

以上を合わせて考えると、問題文の条件は「①が示す円の内部の点全てが②の領域にあればいい」という条件に言い換えられます。
これをさらに言い換えると、「①の円が②の領域の中にある。」...(条件A)ということになり、これがぎりぎり成り立つのは下の図の様になるとき、つまりb/2=aとなるときであり、bがそれ以上大きくなる分には②の正方形が大きくなるだけで条件Aは成り立つので、求めるべきa,bの条件はb/2>=a、つまりb>=2aという風になります。
空間図形の求積問題の図形のイメージ
受講生の質問
空間図形の求積問題で図形をイメージできずに時間がかかってしまうがどうすればいいか。
回答
ポイントは3つ
①模範解答のようにに空間図形を綺麗に描ける必要はない
②断面をメインに考える(2次元に落とし込む)
③具体例からだんだん抽象的な場合を考える
空間図形はイメージできないときは頭の中で考える時間は無駄でしかありません。2、3分考えてもよく分からないようであれば、すぐに式を立てて断面を考え、平面図形として扱ってやりましょう。2次元に落とし込めば何も難しいことはありません。
こういった問題を解くうえで忘れてはいけないことは我々は立体をイメージしずらいので、あくまでも断面を考える形で解答を作るということです。
市販の問題集には大抵、その図形が立体的にどのようになっているかということが載っていますが、それは参考程度のものと捉え、実際にイメージできる必要はない(大学受験でその能力は問われていない=きれいな図形をかけなくても問題は解ける(芸大などは除く))ということを意識する必要があります。
回転体を除く求積問題ではいろいろな断面を考えてみてそれを総合して立体をイメージしてみるとよいです。例えば、円柱は底面方向から見ると円に見えますし、それ以外の方向から見ると長方形に見えます。これをなんらかの平面で切断するとなるとその平面は直線(平行な平面でない限り)に見えることになります。
求体積の問題で重要なのは断面から立体を想像したり、立体から断面を想像したりする能力なのです。
断面を想像するときに x=t などの定数で切った断面が想像できない場合は、極端な断面を考えた後に、具体的な断面を考えると良いかと思います。例えば、 0≦x≦1 の場合には、 x=0 や x=1 のような極端な断面を考えた後に、 x=1/2 のような具体的だが極端ではない値の断面を考えることで段々 x = t で切ったときの断面の遷移の仕方がわかってくるかと思います。
以上、ポイントは3つで
①模範解答みたいに空間図形を綺麗に描ける必要はない
②断面をメインに考える
③具体例からだんだん抽象的な場合を考える
ということです。
立体の体積問題
受講生の質問
y=x-1とy=x^2-2x-1で挟まれた部分を底面とし、x軸に垂直な断面が常に正三角形であるような立体の体積を求めよ。
回答
体積の問題は、「適切な軸に沿って、その軸に垂直な平面で切る + 断面での面積を求めて、それを積分する」という2つの手順を踏めばOKです。この問題でも、まずは「適切な軸」を探すところから始めましょう。
「適切」というのは、後の手順が楽になるような、という意味です。つまり、断面がわかりやすかったり、面積を求めやすかったりするような軸のことです。例えば回転体の体積では、回転軸を「適切な軸」に設定すれば、断面が必ず円になり、簡単な計算で断面積を求められます。この問題での「適切な軸」は、x軸に当たります。なぜならx軸に垂直な平面で立体を切ると、断面が正三角形になって容易に面積を求められるからです。 あとはこの断面積をx軸に沿って(=xで)積分すると体積が出てきます。
非回転体の体積
受講生の質問
Xyz空間において、動点P(0,0,(1-s)**2),Q(s**2,1,0)がある。変数sが|s|≦1をみたす実数の範囲を動く時、線分PQが動いてできる局面をSとし、 Sと平面x=yが囲む部分の体積をVとする。Vの値を求めよ。この問題の図が知覚的に捉えられませんでした。
あと、回転体の場合は回転軸と垂直に切るのが定石ですが、非回転体の場合はどの軸に垂直に切るかは試すしかないのでしょうか?
回答
まず今回の問題を最初から説明していくのですが、sという字を用いて直線を表してこれとx=y平面との囲まれる体積を求めよとの問題です。具体的な直線の移動などは分かりませんが、わかりやすい数値s=-1,0,1などを代入してなんとなくの形だけはわからないか試してみましょう。
Sを動かしてなんとなく直線の動き方を考えるとx=yという平面が基準となっていたことが分かります。最初に問題を読んだときはx=yという珍しい切り方をしていたので一瞬ヒヤッとしますがこの平面で切っていた理由が分かりました。
ただしここからが問題で具体的な図の形は見えないので、わかりやすい平面で切って平面図形として考えようという方針に持っていきます。
どの平面で切れば良いかについては後述しますが今回の問題ではy=tという平面で切ると計算がしやすくなります。この平面でsの値を変化させていくと曲線が描けます。あとはこの平面において囲まれている部分がどこかを見つけてあげて、底の部分の面積を求め、tを動かして積分すればいいといういつもの方針になります。
では囲まれている部分がどこかという話ですが今回はx=yと囲まれている部分をそもそも考えていて、y=tで切っているのでx=tで囲まれている部分を求めればいいです。
最後に切る平面の選び方ですが、切った平面と動く直線との交点の座標が表しやすいかどうかで決めます。交点の座標をベクトルを使って表すと計算がしやすく、その計算が簡単になるような切り方を選んで上げましょう。もちろんどの平面で切っても最終的な計算は合うはずではありますが、計算の複雑さや計算量には大きな差が出ます。
求積問題の変数の設定
受講生の質問
質問: 数Ⅲの求積問題で,自分で変数をおくというのがよくわかりません。どうやったら自分でできるようになりますか。
回答
変数を自分で設定するというのは,たとえば「ここからここまでの距離をaとする」とか「ここの 角度をθとする」とかいう操作のことです。これは今まで自然に行ってきたはずで,その時何のために設定したのかといえば,その量(長さや角度)を何か文字で表す要求がどこかにあったからですね。求積問題でもそれは同じです。
さて,面積や体積を求めるのには積分を使います。たとえば断面積を積分すると体積という意味を持った数値が得られるわけですが,どうしてこの操作で体積を求めたことになるのか説明できますか。少し考えてみてください。
積分の本質は細かく切って足し合わせることです。この切り方がポイントで,面積を出す時も体積を出すときも,軸に対して一定の向き(特に,垂直)でないといけません。 面積を例に考えてみましょう。面積を出す時は,その領域を短冊状に切って,一本一本の面積を 出したのちに,足し合わせるのでした。(この操作が,区分求積法により定義される積分に一致するわけです。)この短冊の形は,面積を出すのですから,普通長方形になるようにするのが便利なわけです。(特に関数y=f(x)とx軸との間の領域の面積を出す際には,長方形型の短冊の高さ がそのままf(x)の値(y座標)に一致するので,中でも簡単に計算できるのです。)
なお,垂直でない切り方をすると短冊は平行四辺形になります。この面積はを出すには,横の辺 の長さをそのまま使うわけにいかないので,ひと工夫(√2でわる など)必要になるのです。普通は軸に対し垂直になるように分割していきます。
よって,何か面積や体積を求める時には,何を軸にして(その軸に垂直な線・平面で)分割するのかということが極めて重要になってきます。積分の向きといってもいいでしょう。いずれにせよ,どういう平面で切り分け,足すのかということは任意(自分で決められる)なわけです。そしてこの軸は,積分操作においては積分変数に対応します。x軸方向のちょっと分の幅・厚みという のがdxという記号の意味なのでした(区分求積の解説を確認しましょう)。d● の部分に何の文 字を入れるのか,どの方向の長さを使うのかというのを,自分で設定するわけです。
この設定の仕方にはそれなりに定石があり,例えば
・回転体では回転軸と同じ向きにするしか道がありません(他には,円柱の場合には底面に並行な向き(断面が長方形になるから)
・対象面を複数持つ図形ではその交わりに垂直な向き(断面に並行直線が現れるので)など。
とりあえず回転体の時だけ覚えればよく,回転軸の向きに積分変数となる文字(距離を表す変数)を設定して(つまり,適当な点を基準にとり,その点から回転軸と並行な方向へ測った長さを文字でおく。座標軸と同じイメージ),その軸に垂直な平面で図形を輪切りにして断面積を求め,積分計算を行えばいい,と押さえておけば,自分でもできるようになるでしょう。
連続した整数の積のシグマ
受講生の質問
「Σk(k+1)を求める途中でk(k+1)=1/3{k(k+1)(k+2)-(k-1)k(k+1)}という式が出てきたのがよくわからない」
回答
実はこのやり方はけっこう有名なので、使えたほうがいいと思います。実際、k(k+1)=k^2+kと展開してk^2のシグマとkのシグマを求めて足すより計算量は少ないので実践的に見ても優れたやり方です。
これは、シグマの中身を「1個先のやつから1個前のやつを引く」形にするという解法の1形態です。たとえば、Σ[k=1~n](1/(k+1)-1/k)という和を具体的に書き下してみると「(1/(n+1)-1/n)+(1/n-1/(n-1))+…….+(1/3-1/2)+(1/2-1/1)」となり、間が全て打ち消し合い、最初と最後の「1/(n+1)-1/1」だけ残るというやつです。
今回の変形も、「1個先のやつから1個前のやつを引く」形になっていますよね。なので答えがラクに(少ない計算で)求まるというわけです。
一般的に、いくつかの連続した整数の積(今回でいうと2つ)がシグマの中身に来ているときは、それらのなかで1番大きい数より1大きい数をつけくわえたものから1番小さい数より1小さい数を付け加えたものを引く形に変形すると、シグマの中が「1個先のやつから1個前のやつを引く」形になって、バァーっと間が消えていって最初と最後だけ残るパターンに持ち込めます。
例えば、シグマの中身が(k-1)k(k+1)(k+2)(これは連続する4つの整数の積ですよね)とかだったら、(k-1)k(k+1)(k+2)=1/5・{(k-1)k(k+1)(k+2)(k+3)-(k-2)(k-1)k(k+1)(k+2)}と変形でき、間が消えていくパターンに持ち込めます。
逆像法の使い方や意味
受講生の質問
逆像法の使い方や意味がいまいち掴めません。
回答
逆像法は関数によって変換された結果(像)から、元の入力(逆像)を復元するというも のです。
逆像法を用いる方法で、簡単な例から考えてみましょう。
例1)関数f(x)=x^2+1 において、f(x)=10 となる xの値を求めなさい
答え1)x=3,-3
例2)xが実数全体を動く時、y=x^2-2x+1がとりうる値の範囲を求めよ
考え方)
この問題では、結論から言うとy>=0ならば実数xが存在できるということが言えるのですが、
具体的に、y=4,1,0のときなどを代入してxについての方程式を解いてみると実際に実数解xを持
つということがわかると思います。
例えば、y=1の時 x^2-2x=0よりx=0,2などです。
逆に、y=-1,-3などを代入するとxは実数とならないことがわかると思います。
答え2)xについての二次方程式x^2-2x+1-y=0が実数解を持つので、
判別式D/4=1-(1-y)>=0
よってy>=0
☆範囲を求めたい文字(今回はy)を定数に見立てて、存在条件や範囲がわかっている文字(パラメータ)についての方程式と見立てるという手順で逆像法は行います。
例3)直線y=2ax+a^2…①について、-1<=a<=1の時、①が動く領域を図示せよ
答え2)同じようにこの問題では、yを定数に見立てて、範囲のわかっているaについての方程式と
見立てます。
そうすると、a^2+2xa-y=0
これが-1<=a<=1に実数解を少なくとも一つ持つ条件を考えると、左辺をf(a)として、
i)①が-1<=a<=1に二つの実数解を持つとき
f(-1)>=0かつf(1)>=0
軸:-1<=-a<=1
判別式:D>0
ii)①が-1<=a<=1にただ一つの実数解を持つとき
f(-1)・f(1)<=0
i)ii)の領域を表す。
という流れになります。
ポイントは上記のように、パラメータの文字についての方程式と見立てることでパラメータを消去
し、動く領域を求めたい文字の範囲に変換することです。
逆像法の考え方
受講生の質問
数学の逆像法について質問です。
例えば
aが0≦a≦1の範囲で変化するとき曲線群C:
y=x*2+ax+a*2の通過する領域を図示せよ。
という問題で、パラメータaに関する二次方程式だから0≦a≦1の範囲に1つだけ解をもつときと
2つ解を持つときの2通りの状況があるけど、
aの実数解が0≦a≦1の範囲に1つある場合と2つある場合の違いがなんなのかよくわかりません。
回答
逆像法の考え方の難しいところです。 メールで送ってくださった問題を具体的に考えていきます。 「aが0≦a≦1の範囲で変化する時のy=x**2+ax+a**2の動く範囲」というのは 「もし、点(X,Y)がこの領域に入るならば、Y=X**2+aX+a**2という関係をみたす 0≦a≦1のaが少なくとも1つある」ということと同じです。 ⇔「y=x**2+ax+a**2をaについての2次方程式と見た時に0≦a≦1の範囲で少なくとも実数解を一つ持つ」とも言えます。 具体的な点を見てみて、点(1,2)を考えます。
2=1+a+a**2を解くと0≦a≦1のaが一つあるので求める領域の中に点(1,2)はあります。 他の点(-1,1)ではどうなるかというと 1=1-a+a**2を解くと0≦a≦1の範囲に2つ解があって条件を満たすaが存在するので求める領域の中に 点(-1,1)があると言えます。
どちらの場合でも条件は満たすのですがaの範囲にあるaの個数は異なります。 結局、少なくとも一個aが存在すればいいというのが2つの場合を考えている理由です。 下線部の言い換えが重要です。
順像法と逆像法のどちらで解けばいい?
受講生の質問
軌跡と領域の範囲の、関数の通過領域を求める問題で、順像法と逆像法のどちらで解けばいいかをいつも迷ってしまう。 どうすれば良いでしょうか。
回答
最初に考えるべきなのは、逆像法です。
なぜなら、順像法の場合、動かす変数に応じて変化する関数の挙動が見えにくいことが多いからです。
例えば、y=ax^3+(a^2)x^2+1という関数をaを実数として動かしたときの通過領域は、順像法でaを動かして3次関数の挙動を見ようとしてもまず不可能です。
さらに、逆像法のメリットとして、厳密性がある、ということです。
順像法の場合、直線以外の関数を動かした領域を図示した時、たとえ正しくてもその厳密性を言葉で表現しづらいことがあります。 以上の理由から、まず逆像法で考えてみて無理そうなら順像法で考えます。
順像法の逆像法に対するメリットとしては、より早く解ける場合がある、ということです。 例えば、y=m(x-1)をmを-2から3の範囲で動かす。といった問題は逆像法なら移項し、mの存在条件を考える必要がありますが、順像法なら5秒で通過領域のイメージが湧きます。 この問題は逆像法でも解けますが、問題によっては逆像法では不可能な場合もあるので適切な解法の選択は重要です。
解法選択の練習として、片方の解法で解けた問題をもう片方でも考えてみて、解けるのか、それとも不可能か、また適切な解法がなぜその方法なのかを考えると良いです。
平面図形
受講生の質問
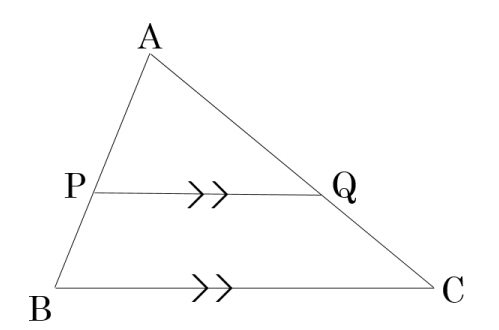
辺BC,PQは平行
△ABCの辺AB,AC上にそれぞれ点P,Qが存在する
この時、次のことが成り立つ
ただし、③の逆は成り立たない。
①BC∥PQ⇔AB:AP=AC:AQ
②BC∥PQ⇔AP:PB=AQ:QC
③BC∥PQ⇒AP:AB=PQ:BC
教科書等には一般にこのように書かれていますが、 「③の逆は成り立たない」のはなぜですか?
回答
図をまず見てください。
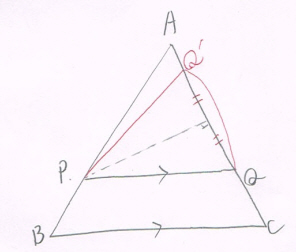
AP:AB=PQ:BCが成り立つとき、図のPQについては、確かにPQ//BCが成り立ちます。
しかし、AC上でPQ=PQ' となるような別の点Q'を取ることが出来るのです。
この場合、AP:AB=PQ':BC が成り立っていながら、PQ'//BC は成り立っていませんね。
このように反例があるため、逆は成り立たないのです。
極限
受講生の質問
√(x^2 + x) + xのx→-∞の極限を求める際、x=-tと置き換えないで計算すると、
=(x^2 + x - x^2) / [√(x^2 + x) - x ]
=x / [√(x^2 + x) - x ]
= 1 /[√(1 + 1/x) - 1 ]
となり、極限が1/(1-1)=1/0になってしまい、置き換えた場合と解答(-1/2)と異なってしまいます。なぜそうなるのかわかりません。
回答
非常にいい質問であり、とても多くの受験生が間違えるところであります。 以上の式変形をしていただいたのだと思いますが、どこが誤りなのでしょうか。
√(x^2 + x) + x
=(x^2 + x - x^2) / [√(x^2 + x) - x ]
=x / [√(x^2 + x) - x ]
ここまでは何の問題もありません。問題はこの後
= 1 /[√(1 + 1/x) - 1 ]
としたところです。ここが誤りです。
x / [√(x^2 + x) - x ]の分母をxで割って、
1 / [√(x^2 + x) / x -1]とし、√の中に1/xを入れて1/x^2として
1 / [√[(x^2 + x)/x^2] -1]
としたのだと思いますが、これが誤っているところです。
今、x→-∞を考えているので、x<0です。負の数は√の中に入れることができません。
x / [√(x^2 + x) - x ]
= 1 / [√(x^2 + x) / x -1]
ここまではいいですが、このあとxを√の中に入れる際にそのままでは入れることができません。
そこで、xが負の時-xなら正ですので、-xを中に入れます。
√(x^2 + x) / xにおいて、x=-(-x)として、この(-x)を中に入れます。
√(x^2 + x) / -(-x)
=- √(x^2 + x) / (-x)
=- √[(x^2 + x)/(-x)^2]
=- √(1+1/x)
となります。
1 /[ - √(1 + 1/x) - 1 ]
となりますから、x→-∞とした時この極限値は1/(-1-1) = -1/2となり、置き換えた場合と一致します。
このように√の中に負の数を入れる時には、そのままでは入れられないというのをよく忘れます。
私たちは負の数の操作に想像以上に慣れていません。
このようなミスを防ぐために、原則的にx→-∞の時にはもうt=-xと置き換えてしまうのが安全だと言われています。
確率の問題へのアプローチ法
受講生の質問
確率の問題で方針が思い浮かばない時、どのようにすればよいでしょうか?
回答
確率の問題では、方針を考えるにあたって
①「具体的な実験」
②「方向性の決め打ち」
が重要になります。
前者については一般的に言及されていることかとは思いますが、実験を行うことは問題文の理解を深めることと解法の糸口を見つけることにつながります。
一方で、後者の「方向性の決め打ち」も非常に重要です。
例えば、最終的に求めたい形や答えの形式がなんとなくわかりそうであれば、それに基づいてどのように考えるべきかを逆算することができます。問題によっては、漸化式を使うべきか、直接確率を求めるべきかといった選択が発生しますが、問題の性質を基にどの方法が適しているかを決め打ちすることが、解法の見通しを立てる助けになります。
これらの手法を併用することで、確率問題に手をつけ始めやすくなり。自然と実力が向上していくでしょう。
確率 排反と独立
受講生の質問
確率の分野なのですが、排反と独立の違いが明確にわからないです。
明確な違いを教えてください。
回答
排反と独立は、確率を求めるときにキーになる二つの考えですね。この二つは、実際全く異なる概念です。定義と具体例を確認しましょう。
排反というのは、いくつかの事象が同時には起こらないことを言います。AとBが排反なら、AかつBが起こる確率は0です。例えばコインを投げて表がでる事象と裏が出る事象は排反です。
一方で、独立というのは、高校数学だと多くは「試行」に対して使われてそれぞれの試行が関係しないこと、互いに試行の結果に影響を及ぼさないことをいいます。試行aとbが独立と言われたら、aの結果がどうであろうと、bの結果には影響しません。
例えばガチャポンで1回目に出たものが低レアの景品だった場合、2回目は高レアの景品が出る確率が高まります(分母が減るからです)。この場合は1回目と2回目は独立ではありません。一方で、ソシャゲ(ソーシャルゲーム)の電子ガチャの場合は、何度回しても高レアの排出率は一定ですから、この場合1回目と2回目は独立な試行ということになります。
確率を求める文脈では割と同格に扱われることが多いので混乱してしまうのかも知れません。ですが定義を確認すれば、上のようにかなり違う概念なんだと分かってもらえると思います。実際に問題を解くときにも、どちらを使えばいいか分からなくなったら定義に戻って考えるといいでしょう。
確率、場合の数の数え上げのポイント
受講生の質問
「赤玉2個、白玉3個の入った袋Aと赤玉1個、白玉4個の入った袋Bからそれぞれ同時に2個ずつ取り出す。取り出した赤玉が合わせて2個以上になる確率を求めよ」という問題の模範解答で、「Aから2個、Bから1個」のような場合を考えず、1/10+6/25としている考え方がわかりません。
回答
確率、場合の数の最も重要なポイントのひとつはもれなく、だぶりなく数えることです。ですがこれを頭が整理された状態で実行するのはなかなか難しいことです。そこで場合分けの仕方がポイントになってきます。一度に考えるのではなく、階層構造を作るようにして、上位の階層から順番に考えてみましょう。
この問題ではまず「Aから赤玉をいくつ取り出すか」に着目しています。これが最上位の階層です。Aからの赤玉の個数としてあり得るのは0,1,2個で、このうち0個の時は絶対条件を満たさないので(Bに1個しか赤がないから)考える必要がありません。よって「Aからの赤玉」の階層での場合分けは(i)2個 (ii)1個の2通りで、これでこの階層ではもれなくだぶりなく状況をあげたことになります。 次に、(i)(ii)それぞれで「Bから赤玉をいくつ取り出すか」を考えます。ありうる個数は0か1です。(i)では、すでに赤玉が2個供給されているのでBからの赤玉が1個でも0個でも条件を満たします。(ii)ではBから赤玉を1個取り出すときだけ条件を満たします。 よって、求める確率は、(i)は「Aから2個取り出す確率」×「Bから赤玉を0個か1個取り出す確率(これは1です)」となり、(ii)は「Aから1個取り出す確率」×「Bから赤玉を1個取り出す確率」となります。この合計が答えです。
このように、条件のどこかに着目し(今回はAの個数)、まずそれだけで場合分けした後で、各場合について考えるようにするといいでしょう。はじめに着目する条件はなるべく強いもの(影響の大きいもの)の方がいいです。 (i)では、Bの取り出し方に関わらず条件を満たす、つまり「それ以上状況を考えなくていい」場合が現れました。このようなことは「(i)A2個B1個 (ii)A2個B0個(iii)A1個B1個…」のような平板な数え方では起こり得ず、順番に処理することのメリットのひとつと言えます。強い条件から考えようということの理由はここにあります。強いものを最初にした方がその後の場合分けの手順が省けることが多いのです。
ボールと箱を区別する場合の箱への入れ方の問題
受講生の質問
ボールと箱を区別する場合の箱への入れ方の問題について、なぜボールと仕切りと同様の発想で問題を解いてはいけないのか
回答
<ボールを区別しない場合の考え方>
ボールを区別しない場合、注目すべきは「ボールの数」です。この状況では、箱を主体に考え、それぞれの箱に何個のボールが入るかを考察します。問題解決には仕切りを使用し、どのボールがどの箱に入るかは考慮しません。
<ボールを区別する場合の考え方>
ボールを区別する場合、ボールの数は重要ではなく、「それぞれのボールがどの箱に入るか」が重要になります。ここでは箱ではなくボールが主体となります。したがって、仕切りに基づく解法は適用できず、各ボールがどの箱に入るかを考えることが適切なアプローチとなります。
ボールと箱の問題では、ボールの区別の有無が解法に大きく影響します。ボールを区別するか否かによって考え方が変わるため、文章から聞かれていることを読み取り。正しいアプローチを選択することが重要となります。
次数がわからない関数を含む恒等式の場合分け
受講生の質問
[問題]
n次式であるf(x)が
(x+1)f '(x)-3f(x)+2x-1=0
f(0)=1
という関係を満たしているとき、nとf(x)をそれぞれ求めよ。
この問題を解くとき、nと1の大小で場合分けをする必要があります。
では、なぜその場合分けをしなければならないか説明することができますか?
[受講生の実際の質問]
nと1の大小で場合分けをするというのが理解できていません。
回答
一般に、n次式を微分するとn-1次式になります。よってf(x)がn次式ならf '(x)はn-1次式です。 これは大丈夫ですね。
本問のように次数のはっきりしない恒等式の問題では、最高次数の項を比較するのが常套手段です。
(x+1)は1次式ですから、(x+1)f'(x) は1+(n-1)=n次式、-3f(x)はn次式、2x-1は1次式です。
したがってn≧2であれば、最高次数であるn次の項をもつのは(x+1)f'(x) と-3f(x) ですから、この2項について、それを展開した中でのn次の項を比較すれば済みます。
しかしn=1のとき、最高次数である1次の項をもつのは、(x+1)f'(x) , -3f(x) のほかに2x-1も含まれます。 よって比較すべき項が増えます。
このように、n=1とそれ以外の時で、最高次数の項を比較する際考慮する項が異なるので、場合分けをしなければいけません。
因数分解
受講生の質問
2cos2x + 8sinx -5 ≦0
を因数分解したあと
(2sinx-3)(2sinx-1)≧0
からわからなくなってしまいました。
回答
非常に良い質問です。
少し戻って、
(2sinx-3)(2sinx-1)≧0
から説明しましょう。ここから実は2つの考え方があります。
1つ目は以下のようなものです。
2sinx-3の符号について考えて見ましょう。
sinxはどんなに頑張っても最大値1までしかいけません。ということは、
2sinx-3の最大値は-1ということです。つまり、2sinxは常に負です。
よって、(2sinx-3)(2sinx-1)≧0
というのは、常に2sinx-3<0であることを考えると両辺を2sinx-3で割ることができて(0ではない、かつ符号がわかってるので不等号の向きの変化がわかるため)
2sinx-1≦0となります。
あとはここからsinx≦1/2として解いていけば良いです。
さて、2つ目は○○さんのやっていただいたように、
(2sinx-3)(2sinx-1)≧0から
sinx≦1/2 または sinx≧3/2
とするものです。(この「または」が地味に大事です。意識していましたでしょうか?)
sinx≦1/2を満たすxは0≦x≦π/6または5π/6≦x<2πで良いと思います。
sinx≧3/2をみたすxはどうでしょうか?
上述の通り、sinxはどんなに頑張っても最大値は1までしかいけません。よって、sinx≧3/2をみたすxは存在しない、というのが正しいです。
sin(π/2+θ)やcos(π-θ)の変形
受講生の質問
sin(π/2+θ)やcos(π-θ)の変形が覚えられません。
何かいい方法はあるでしょうか?
回答
この類の変形は暗記すべきではありません。暗記するにはパターンが多すぎますし、似た形が多くて符号のミスが頻発します。 なので、一元的に考えられる方法を習得すべきです。
大きく分けて2通りの方法があります。できれば両方を習得すべきですが、難しかったらまずは片方だけでもいいので習得しましょう。
・加法定理の利用
・単位円の利用
の2通りです。
①加法定理の利用
sin(a+b)=sin a cos b+cos a sin bなどの加法定理をそのまま使います。
例えばsin(π/2+θ)であればπ/2をa,θをbと見かけて上の公式を使うと
sin(π/2+θ)=sin(π/2) cosθ +cos(π/2) sinθ=1×cosθ +0×sinθ=cosθ
となります。
cosならcosの加法定理を使いましょう。tanでも同様です。
②単位円の利用
単位円を使って考えます。
ポイントは
・θ=10°くらいで考える(45°くらいだとsinとcosの見分けがつきにくいので、なるべく極端な角度で考える)
・sinなのかcosなのか、-がつくのかつかないのか の2視点で考える
です。
実際に考えてみましょう。
θ=10°くらいで考えてみます。
下の図を見てください。sinθは結構小さく、cosθは結構大きい(1に近い)です。

このような状態です。cosθがx座標、sinθがy座標なのも確認しておきましょう。
では、sin(π/2+θ)がどうなるのかを考えてみましょう。
π/2+θということは、θをπ/2=90°回転した点になります。sin(π/2+θ)はその点のy座標になります。
図的には

となります。赤字のsin(π/2+θ)がどうなるのかを考えたいのです。
sinなのかcosなのか、-がつくのかつかないのか の2視点で考える というのがポイントなのでした。
sinなのかcosなのかについては大きさに注目します。
上の図をみるとsin(π/2+θ)は結構1に近く、大きいです(対照的にcos(π/2+θ)は小さめです)
大きめなのはsinθとcosθのどちらだったかというと、cosθのほうなのでした。
なので、cosθの形になるとわかります(符号はこの時点では不明です)
次に-がつくのかつかないかを考えます。
これは単純にsin(π/2+θ)が負なのかどうかに注目します。
上の図をみると明らかに正の場所にあります。なので、マイナスがつかないとわかります。
以上を合わせるとcosの形であり、かつマイナスがつかないので、sin(π/2+θ)=cosθ だとわかります。
同様に考えるとcos(π/2+θ)は小さめ=sinの形であり、かつ負の位置にある=マイナスがつくので、cos(π/2+θ)=-sinθ だとわかります。
tanに関しては単位円で考えてもいいですが、tanθ=sinθ/cosθの変形をして分母と分子のそれぞれのsin,cosについて変形するのがおすすめです。
説明を読んだだけでは使えるようにはならないので、以下の表を埋めて練習してみてください。

答えは

となります。
慣れてきたら、+2π=2π回転=1回転なので、単位円で考えると、結局元の位置に戻ることを利用して、
+3πは+(3π-2π)=+πと同じだ
といったような考えたかたもできるようになりましょう。
加法定理を使う考え方はシンプルですが多少時間がかかります
単位円を使う考え方では慣れるまでは厄介ですが、慣れたら一瞬でできます。
どちらかというとおすすめは単位円を使うほうです。
数列の一般項
受講生の質問
{an},{bn}の一般項をそれぞれan=2^n, bn=3n+2とする。{an}の項のうち、{bn}の項を小さい方が順に並べて得られる数列{cn}の一般項を求めよ。 という問題で、模範解答が途中からわからなくなりました(実際にはより具体的にその箇所が指摘されています)。
回答
2つの数列 an = 2^n bn = 3n+2
のうち、一致している項のみを取り出すと一般項はどう書けるかという問題です。
この場合は、まずanの何項目とbnの何項目が一致しているかを調べる必要があります。 それがわかれば、あとはそれをanかbnのどちらかの式に代入すればcnが求まります。
よって、今anのl項目がbnのm項目に等しいとしてlとmの関係を求めます。
al = bmですから、
2^l = 3m+2です。
さて、これをこのまま解こうとすると左辺は指数関数、右辺は1次式で解くのが難しいです。
そこで、直接求めるのが難しい場合は実際の数から予想してから方針を立てるという鉄則に従いましょう。
少しanとbnの項を書き出してみましょう。
an = 2, 4, 8, 16, 32, 64, 128
bn =5,8,11,14,17,20,23…,32…
よって、かなり雑ではありますが、8,32が一致してますのでもしかしたらanの項が1個おきに一致しているのではと思います。 そこで、実際に128も一致しているかをみると、 128=3n+2 を解けばn=42とできますので、bnも48項目に128があり、一致してます。
いよいよanの一個おき(初項は8)にanとbnが一致していそうなので、これをcnと予想します。
cn=8,32,128,…つまり、cnは初項は8、公比は4の等比数列と予想できます。
あとは、これを証明するだけです。
i) 初項8は一致している。
ii) anのl項目とbnのm項目が一致していると仮定した時、anのl+2項目もbnのどこかに一致していることを示す。
al = bmですから、
2^l = 3m+2です。この時、
al+2
= 2^(l+2)
= 4× 2^l
= 4× (3m+2) (仮定を使った)
= 12m + 8
= 3(4m+2) +2
よってal+2 = b4m+2なので、確かに一致する項がある。
ゆえに、anのl項目とbnのm項目が一致していると仮定した時、anのl+2項目もbnのどこかに一致していることが示された。
i)ii)より、数学的帰納法からcnは初項8、anの2つおきの項からなることが求まり、cnは初項は8、公比は4の等比数列とわかったので一般項は
8×4(n-1)
=2^(2n+1)
このように、模範解答には予想して数学的帰納法というのがはっきり書いてなかったので分かりにくかったのだと思います。 実際には上記のような思考過程を経ています。
漸近線の変化
受講生の質問
190、192の画像についてです。これらの問題は正の無限大と負の無限大によって、漸近線が変化する問題ですが、この手の曲線であることの判別は、実際に極限を取らないとわからないものなのでしょうか?
※実際の受講生の質問には問題集の問題の画像が添付されていますがここでは割愛させていただきます。
回答
大体の推測をすることはできます。要は、具体的にxに「大きい値」を代入してみて、定数を無視すればどうなるかを考えれば良いのです。
190なら、x=100などを代入してみると、√の中身は、-1などは無視できるので√x^2=x となりますよね。ということはxが十分大きければ2x+x=3xに近づきます。
負ならどうかというと、x=-100 にすれば√の中身は、やはり-1は無視出来て、√(-100)^2=100=-x となります。
よって2x-x=x に近くなるわけです。
常にこのように推測できるわけではないですが、√の中身にx^2が入っている今回のような関数は、上の方法で推測できる場合が多いと思います。
複接線
受講生の質問
204の画像についてです。ここでは複接線というものが取り上げられていますが、これは入試でよく取り上げられるのでしょうか?また対処の仕方としては、どういったものになるのでしょうか?
※実際の受講生の質問には問題集の問題の画像が添付されていますがここでは割愛させていただきます。
回答
複接線という言葉自体はどうでも良いですが、たまに取り上げられることはありますね。 といっても「2点で接する接線の方程式は」とか、しっかり明記されると思います。
今回のような問題で「実は複接線があるから本数≠接点の個数でした~」みたいな落とし穴を作るのは、 難関大学の中でさらに難しい問題で、可能性がある程度の話です。
なのであまり心配しなくても良いですが、グラフの概形を考えられるなら、 一度確認してみるとより盤石ではあります。
積分 面積の最小
受講生の質問
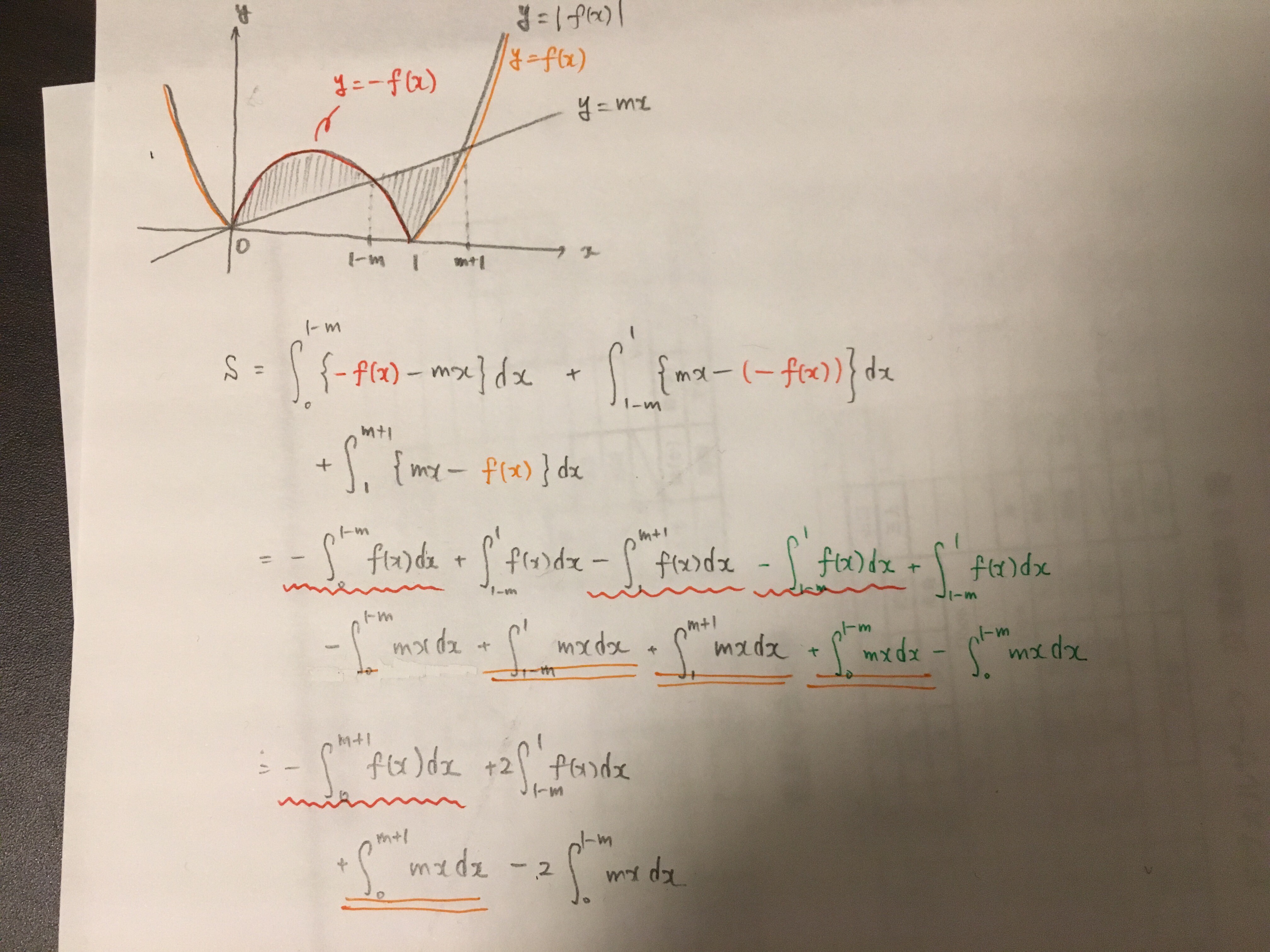
曲線 C : y = |x(x-1)| と 直線 l : y = mxがある。C と l とで囲まれる部分の面積 S を最小とする m の値を求めよ。ただし、C と l は異なる3つの共有点を持つ。
という問題ですが、解説にある一連の式変形が少しこんがらがってしまいます。
この式変形はどうなっているのでしょうか。
回答
添付図を参考にしてください。落ち着いて考えましょう。
計算を楽にする工夫です。あと少しで積分範囲が全部繋がって綺麗になるのに…と思っているとこの式変形を思いつきます。
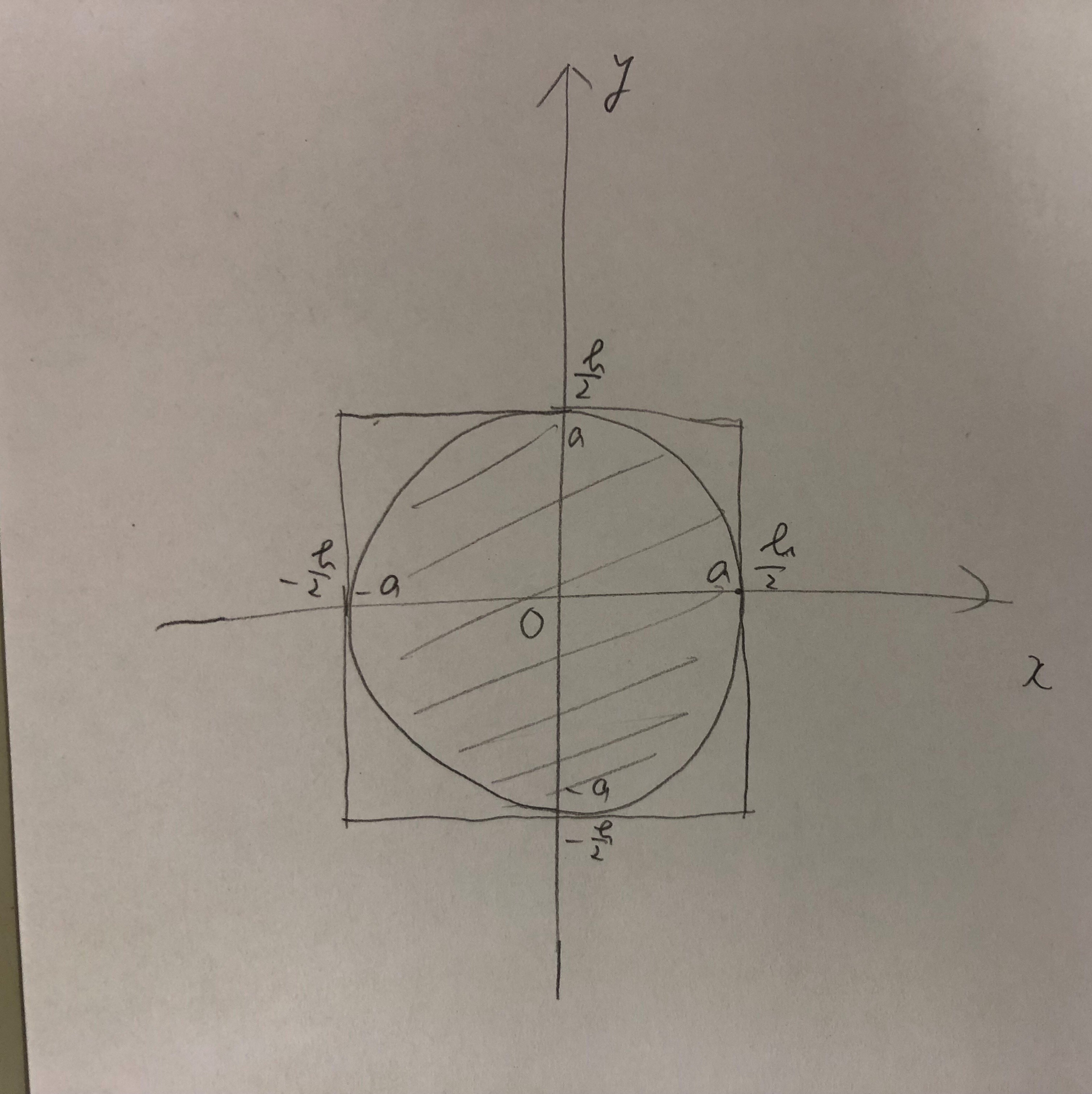
楕円についての理解のポイント
受講生の質問
楕円についての理解が曖昧なのですが抑えるべきポイントはなんなのでしょうか? 公式だけ覚えて問題が解ければそれで良いでしょうか?
回答


複素数問題の解法手順
受講生の質問
「複素数𝑧の範囲を図⽰しなさい」という問題の解答⽅針が定められません。
回答
複素数の問題の解法として
①複素数の性質を使い、𝑧 のまま解く
②複素数の⼤きさと偏⾓を定める(𝑧=𝑟(𝑐𝑜𝑠𝜃+𝑖 𝑠𝑖𝑛𝜃) とおく)
③実数に置き換える。(𝑧=𝑥+𝑦𝑖 とおく)
の3つが考えられると思います。
解答を作成する上での優先順位は①>②>③であると考えています。
特に①は共役な複素数と複素数の実数条件を使う時に有効的です。
③は⼀⾒どんな問題に対しても使える万能な解答⽅針のように思えますが、かなり計算が煩雑になってしまいます。
解答⽅針①で解答を作り始め、①だけでは処理できない条件を導いたところで、②や③の解答⽅針に切り替えるという解き⽅をすることで、それぞれの解答⽅針で扱いにくい部分を避け、計算が楽な解答を作るという⽅針を取るのが良いと思います。
複素数 虚数ωの範囲
受講生の質問
「数学2Bの虚数ωの範囲を、学校では「入試にはほとんどでないからやらなくていい」
と言われたのですが、本当にやらなくていいのでしょうか?」
このコンテンツをご覧いただいている皆さんに質問です
この質問ですが、みなさんが今受けている指導や質問できる人に質問した場合、的確な回答が得られますか?
またみなさんも他の科目や分野でこのような疑問を持ったことはないですか?
安易に語られているゴールから逆算するとか志望校の過去問を見ればわかるというような指導、アドバイスではこの問題には的確に回答できません。
的確なものは絶対に得られません。
回答
ωについては、説明なしで出題されることは無いと思います。
しかし「x^3=1の虚数解をωとする」といった説明があって、それに関する
出題がされるというのは大いにありえます。
また、ここでポイントとなることは、ωに限らず他の複素数でも有用です。 「次数下げ」というテクニックになりますが、応用できますか。
例えば下の問題を解いてみてください。
a= - 1+√2 i とするとき、a^4 の値は?
ヒント:まともに計算しようとすると大変ですね。
そこで、「aが解となる2次方程式」を求めてみてください。
そうすれば28(2)と同じように次数を下げることが出来ます。
指導内容・コース・受講料の詳細はこちらから▼
数学を得意科目にできる個別指導とは
実際の合格の天使受講生の実際の質問回答をご覧いただいてきましたが、 このような回答を得られるかどうかだけでも今後の勉強や受験対策に相当な差がつくことはお分かりいただけると思います。
みなさんもこのような部分で疑問を持ち、まだ基礎標準知識の習得が済んでおらず過去問分析が自力でできない段階では、 質問できる人にしっかり聞いてください。
数学の個別指導に隠された真実
ここではっきりと真実をお伝えしておきますが、大学入試において何をどこまで得ておけばいいか、考えておけばいいのかという線引きを明確にできるのは、またそれらを踏まえた的確な戦略や勉強法、勉強計画を指導できるのは以下の条件を満たす場合のみです。
2、実際に基礎理論から具体的問題にわかりやすく解答できること
3、実際に全国の大学のどんな問題にも的確に解答できること
という3段階のレベルをすべてクリアーしている実力を有している場合のみです。
もちろん自称ではなくしっかりとした受験結果に実証されていることが大事ということも忘れないでください。
あなたが得ている指導は結果に実証されていますか?
戦略や勉強法や計画だけ語ることは、拝借して行けばいくらでも圧倒的実力者と同じことを語れます。
しかしそれは決して的を射た的確なものではないことは本来説明するまでもないことです。
医学部の数学や物理、化学、生物など理系学部の具体的な問題について基礎理論から解説・解答できないにもかかわらず、
また自身が実際にその次元での合格という結果を出していないにもかかわらず、
戦略や勉強法、勉強計画だけが優れたものになることなど絶対にありえません。
自身の受験結果に実証されている高い実力がある指導者から指導を得られるか否かだけで、 実際の勉強効率、成績の伸び、さらには狭き門である医学部,難関大の合否まで決まっている側面があるのも事実です。
以上、受験の真実を本音をお伝えしました。
これをご覧いただいている皆さんは、本気になって合格へ向かってください。
数学の成績が伸びない・勉強の効率が上がらない核心的な理由
みなさんはやる気の問題や勉強効率の問題に悩まされたり、 塾や予備校で一般的な問題解説講義を受けても自分のわからないところを解決できない、 深く理解できない、ということを感じたことはありませんか? これは多くの受験生が悩まされたり感じていることです。
でも、
■やる気や勉強効率を大きく阻害する「わからない」「できない」ところを日々解決していけるとしたら
■しかも、自分のわからない部分を圧倒的実力者が丁寧に説明してくれて理解していけるとしたら
■さらにそれが、受験数学を高いレベルで極めた人間のみがなしうる、他の問題にも通用する思考を伴った説明・解説とともに入試に必要なレベルで過不足なく得ていけるとしたら
■さらにさらに、受験数学のすべての問題を解きうる講師陣から、大学入試においてはここまで理解していれば大丈夫ですという明確な区切りとともに得ていけたら
あなたがやる気の問題に悩まされることは極限まで減ります。
→なぜなら受験勉強のやる気を阻害する最も大きな要因は「わからない」「できない」からです。
あなたが勉強効率に悩まされることはなくなります。
→なぜならこれ以上の効率を得ている受験生は日本全国にいないからです。
あなたの実力は確実に伸びます。
→なぜならこれ以上確実かつ効率的に実力を伸ばせる方法など存在しないからです。
当塾が、圧倒的実力講師陣を指導に当たらせている本当の効果や威力を体感してください。
みなさんが毎日の勉強でわからない問題やあいまいな部分をこのように解決していけるとしたらあなたの実力が伸びない原因はありますか?
以上に掲載してきた質問回答は「ごくごく一部」の質問と回答であり、1人の受講生がたった1週間の質問回答で得られるものよりも少ない量です。当塾の受講生はここに掲載している回答を数学に限らず全教科、 1回に~10問程度、フリーコースの受講生は週に30~100問という量で得ていっているのです。これで実力が伸びないはずがないことはお分かりいただけると思います。
「受験生として実際に具体的に何を指導から得ることが出来るか、指導側がどの次元・レベルで実際何を与えているか」 このことは事実と異なるものを安易に語る人間がいる指導実績・合格実績や口先だけの仮装の実力や指導内容と異なり、決して操作することが出来ない事実、ごまかすことが出来ない事実です。
当塾が合格実績として掲載しているものは、受験戦略や勉強法や勉強計画だけを指導した受講生を一切含んでいません。 各教科の質問回答を継続的に数か月以上行った受講生しか合格実績として公表していません。 ですので一般の指導機関が出している合格実績に引き直せば当塾の合格実績は更なる驚異的な数字になります。
以上が受講生の実力が圧倒的に伸びる合格の天使の指導の秘密の一部であり、 徹底した責任指導・個別指導であるがゆえに少数受講生でありながら医学部医学科,難関大へ驚異的合格率を叩き出している事実と証拠です。
受講の有無にかかわらず、数学を効率的にマスターするために問題集や参考書にどう取り組んでいくべきなのか、 何を得ていくべきなのかをこのページの具体例からしっかりと学んでください。 医学部,難関大に合格するためには数学で高得点を獲得することが必須になります。
